为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求 和
和 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: )
)
(.(本小题满分12分)
已知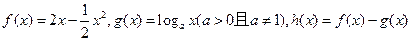 在定义域上为减函数,且其导函数
在定义域上为减函数,且其导函数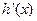 存在零点。
存在零点。
(I)求实数a的值;
(II)函数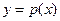 的图象与函数
的图象与函数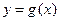 的图象关于直线y=x对称,且
的图象关于直线y=x对称,且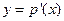 为函数
为函数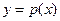 的导函数,
的导函数,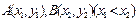 是函数
是函数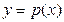 图像上两点,若
图像上两点,若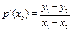 ,判断
,判断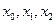 的大小,并证明你的结论。
的大小,并证明你的结论。
((本小题满分12分)
已知F1、F2分别是椭圆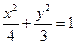 的左、右焦点,曲线C是坐标原点为顶
的左、右焦点,曲线C是坐标原点为顶 点,
点, 以F2为焦点的抛物线,过点F1的直线
以F2为焦点的抛物线,过点F1的直线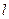 交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
(I)求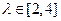 ,求直线
,求直线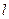 的斜率k的取值范围;
的斜率k的取值范围;
(II)求证:直线MQ过定点。
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在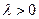 使得
使得 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为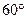 ,求
,求 的值。
的值。
(本小题满分12分)
一次数学模拟考试,共12道选择题,每题5分,共计60分,每道题有四个可供选择的答案,仅一个是正确的。学生小张只能确定其 中10道题的正
中10道题的正 确答案,其余2道题完全靠猜测回答。
确答案,其余2道题完全靠猜测回答。
(I)求小张仅答错 一道选择题的概率;
一道选择题的概率;
(II)小张所在班级共有60人,此次考试选择题得分情况统计表:
| 得分 |
40 |
45 |
50 |
55 |
60 |
| 百分率 |
15% |
10% |
25% |
40% |
10% |
现采用分层 抽样的方法从此班抽取20人的试卷进行选
抽样的方法从此班抽取20人的试卷进行选 择题质量分析。
择题质量分析。
(i)应抽取多少 张选择题得60分的试卷
张选择题得60分的试卷 ?
?
(ii)若小张选择题得60分,求他的试卷被抽到的概率。
(本小题满分12分)
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?