(本小题满分16分)如图是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池 (
( 分别为蓄水池的圆心),经测量,点
分别为蓄水池的圆心),经测量,点 ,
, 到水管的距离分别为55m和25m,
到水管的距离分别为55m和25m, m.以所在直线为
m.以所在直线为 轴,过点
轴,过点 且与垂直的直线为
且与垂直的直线为 轴,建立如图所示的直角坐标系(O为坐标原点).
轴,建立如图所示的直角坐标系(O为坐标原点).
(1)求圆 的方程;
的方程;
(2)计划在水管上的点 处安装一接口,并从接口出发铺设两条水管,将中的水引到
处安装一接口,并从接口出发铺设两条水管,将中的水引到 两个蓄水池中,问点
两个蓄水池中,问点 到点O的距离为多少时,铺设的两条水管总长度最小?并求出该最小值.
到点O的距离为多少时,铺设的两条水管总长度最小?并求出该最小值.
(本小题满分14分)如图,在四棱锥P - ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:
(1)PA∥平面MDB;
(2)PD⊥BC.
(本小题满分14分)某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
(本小题满分14分)已知圆的圆心为坐标原点,且经过点(-1, ).
).
(1)求圆的方程;
(2)若直线 与此圆有且只有一个公共点,求
与此圆有且只有一个公共点,求 的值;
的值;
(3)求直线 被此圆截得的弦长.
被此圆截得的弦长.
设数列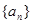 的前
的前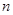 项的和
项的和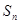 ,已知
,已知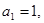
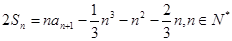 .
.
(1)求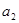 的值;
的值;
(2)证明:数列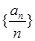 是等差数列,并求出数列
是等差数列,并求出数列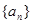 的通项公式;
的通项公式;
(3)证明:对一切正整数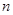 ,有
,有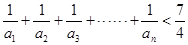 .
.