小明家订了一份报纸，寒假期间他收集了每天报纸送达时间的数据，并绘制成频率分布直方图，如图所示．
（1）根据图中的数据信息，写出众数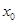
；
（2）小明的父亲上班离家的时间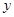
在上午
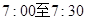之间，而送报人每天在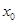时刻前后
半小时内把报纸送达（每个时间点送达的可能性相等）．
①求小明的父亲在上班离家前能收到报纸（称为事件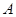
）的概率；
②求小明的父亲周一至周五在上班离家前能收到报纸的天数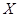
的数学期望．
（本小题满分12分）设函数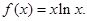
（Ⅰ）设
，讨论函数F（x）的单调性；
（Ⅱ）过两点
的直线的斜率为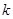
，求证：
（本小题满分12分）已知椭圆
，左焦点到直线x一y一2=0的距离为
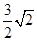，左焦点到左顶点的距离为
.
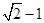（Ⅰ）求椭圆的方程；
（Ⅱ）直线l过点M（2，0）交椭圆于A，B两点，是否存在点N（t，0），使得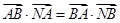
，若存在，求出t的取值范围；若不存在，说明理由．
（本小题满分12分）某市为了对公租房的租金实施办法进行研究，用分层抽样方法从A，B，C三个社区的相关家庭中，抽取若干户家庭进行调研，有关数据见下表（单位：户）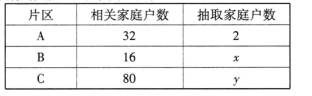
（Ⅰ）求x，y；
（Ⅱ）若从B、C两个片区抽取的家庭中随机选2户家庭参加实施办法的听证会，求这2户家庭都来自C片区的概率．
（本小题满分12分）如图，四棱锥S一ABCD中，已知AD∥BC，∠ADC=90°，∠BAD=135°，
AD=DC=
，SA=SC=SD=2．
（Ⅰ）求证：AC⊥SD；
（Ⅱ）求三棱锥
的体积.
（本小题满分12分）如图，为测得河对岸某建筑物AB的高，先在河岸上选一点C，使C在建筑物底端B的正东方向上，测得点A的仰角为60°，再由点C沿东偏北75°方向走20米到达位置D，测得∠BDC=30°。
（Ⅰ）求sⅠn∠BCD的值；
（Ⅱ）求此建筑物的高度．