如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线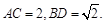 AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.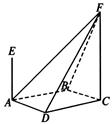
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
(本小题满分12分)
已知 ,点
,点 满足
满足 ,记点
,记点 的轨迹
的轨迹 为
为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)过点F2(1 ,0)作直线l与轨迹
,0)作直线l与轨迹 交于不同的两点A、B,设
交于不同的两点A、B,设
 ,若
,若 的取值范围
的取值范围
(本小题满分12分)
设数列 的前
的前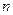 项和为
项和为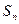 ,且
,且 数列
数列 满足
满足 ,点
,点 在直线
在直线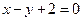 上,
上,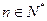 .
.
(Ⅰ)求数列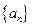 ,
, 的通项公式;
的通项公式;
(Ⅱ)设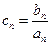 ,求数列
,求数列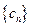 的前
的前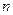 项和
项和 .
.
如图所示,某公园预计在一块绿地的中央修建两个相同的矩形的池塘,每个面积为10000米2,池塘前方要 留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?
留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?
如图,在直三棱柱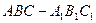 中,
中, ,
, ,
, 是
是 的中点.
的中点.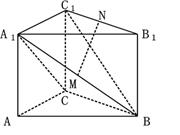
(Ⅰ)在线段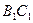 上是否存在一点
上是否存在一点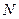 ,使得
,使得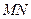 ⊥平面
⊥平面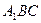 ?若存在,找出点
?若存在,找出点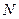 的位置幷证明;若不存在,请说明理由;
的位置幷证明;若不存在,请说明理由;
(Ⅱ)求平面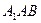 和平面
和平面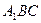 所成角的大小
所成角的大小
(本小题满分12分)
已知△ABC中,内角A,B,C的对边分别为a,b,c,已知a,b,c成等比数列,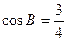 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 的值。
的值。