若数列{an}满足an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”.
(1)设数列{an}为“凸数列”,若a1=1,a2=-2,试写出该数列的前6项,并求出前6项之和;
(2)在“凸数列”{an}中,求证:an+3=-an,n∈N*;
(3)设a1=a,a2=b,若数列{an}为“凸数列”,求数列前2011项和S2011.
已知an=n×0.8n(n∈N*).
(1)判断数列{an}的单调性;
(2)是否存在最小正整数k,使得数列{an}中的任意一项均小于k?请说明理由.
已知数列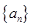 的通项公式an=
的通项公式an=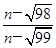 (n∈N*),求数列前30项中的最大项和最小项.
(n∈N*),求数列前30项中的最大项和最小项.
如下表定义函数f(x):
| x |
1 |
2 |
3 |
4 |
5 |
| f(x) |
5 |
4 |
3 |
1 |
2 |
对于数列{an},a1=4,an=f(an-1),n=2,3,4,…,求a2008.
已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.