已知数列{an}成等比数列,且an>0.
(1)若a2-a1=8,a3=m.
①当m=48时,求数列{an}的通项公式;
②若数列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+ +ak+1- (ak+ak-1+ +a1 )=8,k∈N*,求a2k+1+a2k+2+ +a3k的最小值.
在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 ,
,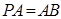 ,点
,点 是
是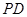 的中点,作
的中点,作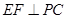 交
交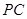 于
于 .
.
(Ⅰ)求证: ∥平面
∥平面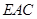 ;
;
(Ⅱ)求证: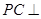 平面
平面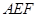 ;
;
(Ⅲ)求二面角 的大小.
的大小.
已知等差数列{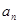 },公差
},公差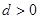 ,
,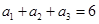 ,且
,且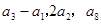 成等比数列.
成等比数列.
(I)求{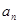 }的通项公式;
}的通项公式;
(II)设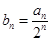 ,求证:
,求证: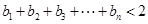 .
.
在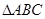 中,内角
中,内角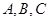 对边分别为
对边分别为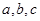 ,且
,且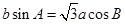 .
.
(Ⅰ)求角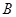 的大小;
的大小;
(Ⅱ)若 ,求
,求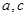 的值.
的值.
(本小题满分14分)
已知函数 (
( ).
).
(1)若 时,求函数
时,求函数 的值域;
的值域;
(2)若函数 的最小值是1,求实数
的最小值是1,求实数 的值.
的值.
(本小题满分14分)
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台. 现销售给A地10台,B地8台. 已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.