已知数列{an}是等差数列,数列{bn}是等比数列,且对任意的n∈N*,都有a1b1+a2b2+a3b3+···+anbn=n·2n+3.
(1)若{bn}的首项为4,公比为2,求数列{an+bn}的前n项和Sn;
(2)若a1=8.
①求数列{an}与{bn}的通项公式;
②试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它r(r∈N,r≥2)项的和?若存在,请求出该项;若不存在,请说明理由.
(本小题满分13分)
如图6,平行四边形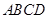 中,
中,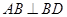 ,
, ,
,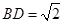 ,沿
,沿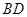 将
将 折
折
起,使二面角 是大小为锐角
是大小为锐角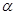 的二面角,设
的二面角,设 在平面
在平面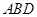 上的射影为
上的射影为 .
.
(1)当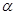 为何值时,三棱锥
为何值时,三棱锥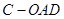 的体积最大?最大值为多少?
的体积最大?最大值为多少?
(2)当 时,求
时,求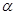 的大小.
的大小.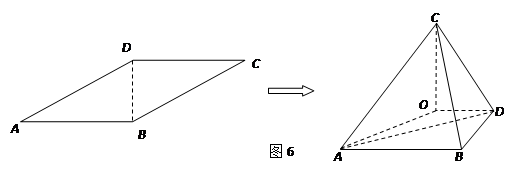
(本小题满分13分)
随机调查某社区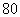 个人,以研究这一社区居民在
个人,以研究这一社区居民在 时间段的休闲方
时间段的休闲方
式与性别的关系,得到下面的数据表:
| 休闲方式 性别 |
看电视 |
看书 |
合计 |
| 男 |
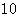 |
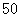 |
 |
| 女 |
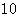 |
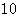 |
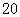 |
| 合计 |
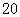 |
 |
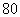 |
(1)将此样本的频率估计为总体的概率,随机调查 名在该社区的男性,设调查的
名在该社区的男性,设调查的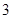 人
人
在这一时间段以看书为休闲方式的人数为随机变量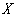 ,求
,求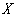 的分布列和期望;
的分布列和期望;
(2)根据以上数据,能否有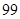 %的把握认为“在
%的把握认为“在 时间段的休闲方式与
时间段的休闲方式与
性别有关系”?
参考公式: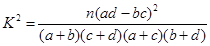 ,其中
,其中 .
.
参考数据:
 |
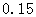 |
 |
 |
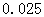 |
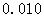 |
 |
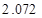 |
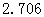 |
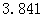 |
 |
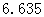 |
(本小题满分12分)
已知函数 ,
, (其中
(其中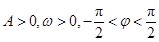 ),其部分图
),其部分图
像如图5所示.
(1)求函数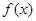 的解析式;
的解析式;
(2)已知横坐标分别为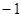 、
、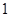 、
、 的三点
的三点 、
、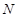 、
、 都在函数
都在函数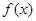 的图像上,求
的图像上,求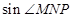 的值.
的值.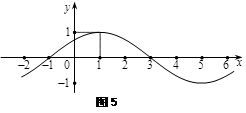
(几何证明选讲选做题)如图4, 是圆
是圆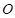 上的两点,且
上的两点,且 ,
, ,
, 为
为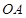 的中点,连接
的中点,连接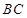 并延长交圆
并延长交圆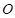 于点
于点 ,则
,则 .
.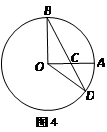
已知等比数列 的首项
的首项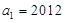 ,公比
,公比 ,数列
,数列 前n项和记为
前n项和记为 ,前n
,前n
项积记为 .
.
(Ⅰ)求数列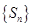 的最大项和最小项;
的最大项和最小项;
(Ⅱ)判断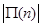 与
与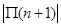 的大小, 并求
的大小, 并求 为何值时,
为何值时, 取得最大值;
取得最大值;
(Ⅲ)证明 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
些等差数列的公差按从小到大的顺序依次设为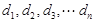 ,证明:数列
,证明:数列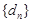 为等比数列。
为等比数列。
(参考数据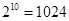 )
)