如图,四棱锥 中,
中, ,
, ,
,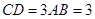 ,平面
,平面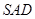 ⊥平面
⊥平面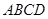 ,
,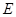 是线段
是线段 上一点,
上一点,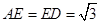 ,
,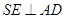 .
.
(1)证明: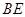 ⊥平面
⊥平面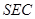 ;
;
(2)若 ,求直线
,求直线 与平面
与平面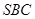 所成角的正弦值.
所成角的正弦值.
已知椭圆 过点
过点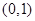 且离心率为
且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)若斜率为 的直线
的直线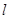 交
交 于
于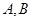 两点,且
两点,且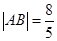 ,求直线
,求直线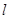 的方程.
的方程.
已知函数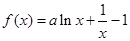 在
在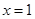 处取极值.
处取极值.
(1)求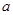 的值;
的值;
(2)求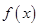 在
在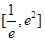 上的最大值和最小值.
上的最大值和最小值.
某研究性学习小组有 名同学.
名同学.
(1)这 名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
(2)从 名同学中选
名同学中选 人参加班级
人参加班级 接力比赛,则同学丙不跑第一棒的安排方法有多少种?
接力比赛,则同学丙不跑第一棒的安排方法有多少种?
已知函数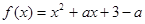 ,
,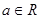 .
.
(1)求 的取值范围,使
的取值范围,使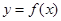 在闭区间
在闭区间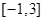 上是单调函数;
上是单调函数;
(2)当 时,函数
时,函数 的最大值是关于
的最大值是关于 的函数
的函数 .求
.求 ;
;
(3)求实数 的取值范围,使得对任意的
的取值范围,使得对任意的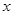
 ,恒有
,恒有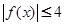 成立.
成立.