如图,在平面直角坐标系 中,点
中,点 ,直线
,直线 .设圆
.设圆 的半径为
的半径为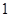 ,圆心在
,圆心在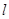 上.
上.
(1)若圆心 也在直线
也在直线 上,过点
上,过点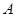 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点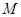 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
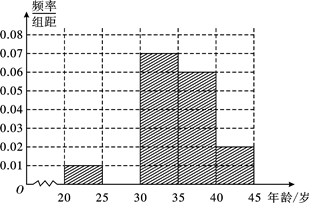
(本小题满分13分)为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
| 分组(单位:岁) |
频数 |
频率 |
| [20,25) |
5 |
0.05 |
| [25,30) |
① |
0.20 |
| [30,35) |
35 |
② |
| [35,40) |
30 |
0.30 |
| [40,45] |
10 |
0.10 |
| 合计 |
100 |
1.00 |
(本小题满分12分)如图所示多面体中,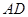 ⊥平面
⊥平面 ,
,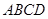 为平行四边形,
为平行四边形, 分别为
分别为 的中点,
的中点, ,
, ,
,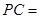
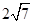 .
.
(1)求证: ∥平面
∥平面 ;
;
(2)若∠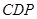 =90°,求证
=90°,求证 ;
;
(3)若∠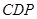 =120°,求该多面体的体积.
=120°,求该多面体的体积.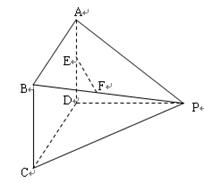
(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,且
,且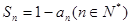 .
.
(1)试求 的通项公式;
的通项公式;
(2)若数列 满足:
满足: ,试求
,试求 的前
的前 项和
项和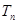 .
.
(本小题满分12分)如图,在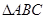 中,点
中,点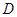 在
在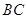 边上,
边上,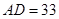 ,
,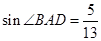 ,
,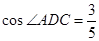 .
.
(1)求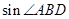 的值;
的值;
(2)求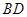 的长.
的长. 
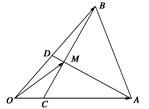
在△OAB中,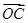 =
=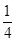
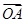 ,
,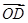 =
=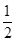
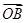 ,AD与BC交于点M,设
,AD与BC交于点M,设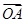 =a,
=a,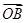 =b,以a、b为基底表示
=b,以a、b为基底表示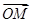 .
.