一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.
(1)求证:AC⊥BD.
(2)求三棱锥E-BCD的体积.
(本小题满分10分)
已知函数 的定义域为A,函数
的定义域为A,函数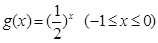 的值域为B.
的值域为B.
(I)求 ;
;
(II)若 ,且
,且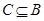 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数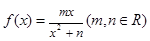 在
在 处取得极值
处取得极值 .
.
⑴求 的解析式;
的解析式;
⑵设 是曲线
是曲线 上除原点
上除原点 外的任意一点,过
外的任意一点,过 的中点且垂直于
的中点且垂直于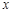 轴的直线交曲线于点
轴的直线交曲线于点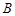 ,试问:是否存在这样的点
,试问:是否存在这样的点 ,使得曲线在点
,使得曲线在点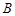 处的切线与
处的切线与 平行?若存在,求出点
平行?若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
⑶设函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求
,求
实数 的取值范围.
的取值范围.
(本小题满分14分)已知定义域为R的函数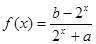 是奇函数.
是奇函数.
(1)求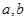 的值;
的值;
(2)用定义证明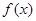 在
在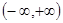
 上为减函数.
上为减函数.
(3)若对于任意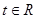 ,不等式
,不等式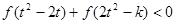 恒成立,求
恒成立,求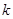 的范围.
的范围.
(本小题满分14分)某种商品的成本为5元/ 件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
|
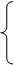
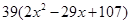
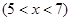 [
[

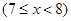 [
[
(本小题满分14分)已知函数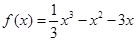 在
在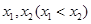 处取得极值,记点
处取得极值,记点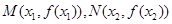 .
.
⑴求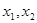 的值;
的值;
⑵证明:线段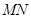 与曲线
与曲线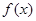 存在异于
存在异于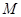 、
、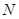 的公共点;
的公共点;