如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
(1)求出体积V与高h的函数关系式并指出其定义域;
(2)问当 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?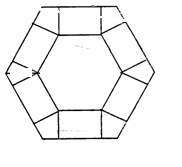
已知抛物线 :
: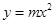 (
( ),焦点为
),焦点为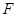 ,直线
,直线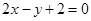 交抛物线
交抛物线 于
于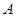 、
、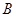 两点,
两点, 是线段
是线段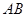 的中点,过
的中点,过 作
作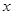 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点 ,
,
(1)若抛物线 上有一点
上有一点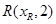 到焦点
到焦点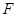 的距离为
的距离为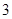 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使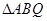 是以
是以 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出
的值;若不存在,说明理由。
已知四棱锥P—ABCD及其三视图如下图所示,E是侧棱PC上的动点。
(1)求四棱锥P—ABCD的体积;
(2)不论点E在何位置,是否都有BD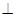 AE?试证明你的结论;
AE?试证明你的结论;
(3)若点E为PC的中点,求二面角D—AE—B的大小。
如图,在四棱锥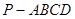 中,
中,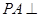 底面
底面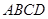 ,
,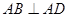 ,点E在线段AD上,且CE//AB。
,点E在线段AD上,且CE//AB。
(1)求证:CE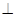 PAD;
PAD;
(2)若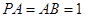 ,AD=3,CD=
,AD=3,CD=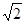 ,
,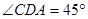 ,求四棱锥
,求四棱锥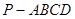 的体积。
的体积。
已知 为坐标原点,
为坐标原点,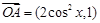 ,
,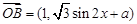 (
(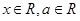 ,
,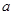 是常数),若
是常数),若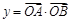 .
.
(1)求 关于
关于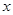 的函数关系式
的函数关系式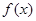 ;
;
(2)若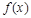 的最大值为
的最大值为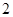 ,求
,求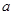 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数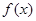 在长度为一个周期的闭区间上的简图,并指出函数
在长度为一个周期的闭区间上的简图,并指出函数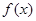 的单调区间
的单调区间
若函数f(x)=sin2ax- sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈ ,求点A的坐标.
,求点A的坐标.