提高过江大桥的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度（单位：千米/小时）是车流密度（单位：辆/千米）的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明：当时，车流速度v是车流密度x的一次函数．
（1）当0≤x≤200时，求函数的表达式；
（2）当车流密度x为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）可以达到最大，并求出最大值．（精确到1辆/小时）．
（本小题满分12分）. 若直线l：
与抛物线
交于A、B两点，O点是坐标原点。
(1)当m=－1,c=－2时，求证：OA⊥OB；
(2)若OA⊥OB，求证：直线l恒过定点；并求出这个定点坐标。
(3)当OA⊥OB时，试问△OAB的外接圆与抛物线的准线位置关系如何？证明你的结论。
（本小题满分10分）. 已知命题p：方程
表示焦点在y轴上的椭圆；
命题q：双曲线
的离心率
；
若“
”为真，“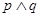
”为假，求实数
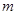的取值范围．
（本小题满分12分）
已知椭圆E的两个焦点分别为F1(－1,0), F2 (1,0), 点(1,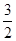 
)在椭圆E上.
(1)求椭圆E的方程
(2)若椭圆E上存在一点 P, 使∠F1PF2=30°, 求△PF1F2的面积.
.(本小题满分12分)
已知直四棱柱ABCD—A′B′C′D′的底面是菱形，
，
E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2.
（1）求证：平面AEF⊥平面AA′C′C；
（2）求截面AEF与底面ABCD的夹角的大小.
（本小题满分14分）
某商店经营的消费品进价每件14元，月销售量Q（百件）与销售价格P（元）的关系如下图，每月各种开支2000元，
（1）写出月销售量Q（百件）与销售价格P（元）的函数关系。
（2）该店为了保证职工最低生活费开支3600元，问：商品价格应控制在什么范围？
（3）当商品价格每件为多少元时，月利润并扣除职工最低生活费的余额最大？并求出最大值。