某超市在节日期间进行有奖促销,凡在该超市购物满200元的顾客,将获得一次摸奖机会,规则如下:
奖盒中放有除颜色外完全相同的1个红色球,1个黄色球,1个蓝色球和1个黑色球.顾客不放回的每次摸出1个球,直至摸到黑色球停止摸奖.规定摸到红色球奖励10元,摸到黄色球或蓝色球奖励5元,摸到黑色球无奖励.
(1)求一名顾客摸球3次停止摸奖的概率;
(2)记X为一名顾客摸奖获得的奖金数额,求随机变量X的分布列和数学期望.
已知f(x)在(-1,1)上有定义,f(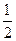 )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(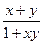 )
)
⑴证明:f(x)在(-1,1)上为奇函数;
⑵对数列x1=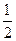 ,xn+1=
,xn+1=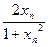 ,求f(xn);
,求f(xn);
⑶求证
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数
f(x)=ax2+bx+1(a>0)有两个相异的不动点x1,x2.
⑴若x1<1<x2,且f(x)的图象关于直线x=m对称,求证: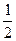 <m<1;
<m<1;
⑵若|x1|<2且|x1-x2|=2,求b的取值范围.
已知双曲线x2-3y2=3的右焦点为F,右准线为l,以F为左焦点,以l为左准线的椭圆C的中心为A,又A点关于直线y=2x的对称点A’恰好在双曲线的左准线上,求椭圆的方程.
过双曲线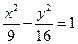 的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离.
的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离.
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|= ,曲线段DE上任一点到A、B两点的距离之和都相等.
,曲线段DE上任一点到A、B两点的距离之和都相等.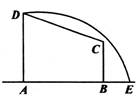
(1)建立适当的直角坐标系,求曲线段DE的方程;
(2)过C能否作一条直线与曲线段DE相交,且所
得弦以C为中点,如果能,求该弦所在的直线
的方程;若不能,说明理由.