如图,在四棱锥P-ABCD中,侧面PAD 底面ABCD,侧棱
底面ABCD,侧棱 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB AD,AD=2,AB=BC=l,E为AD中点.
AD,AD=2,AB=BC=l,E为AD中点.
(1)求证:PE 平面ABCD:
平面ABCD:
(2)求异面直线PB与CD所成角的余弦值:
(3)求点A到平面PCD的距离.
如图,矩形BCC1B1所在平面垂直于三角形AB C所在平面,BB1=CC
C所在平面,BB1=CC 1=AC=2,
1=AC=2,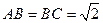 ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。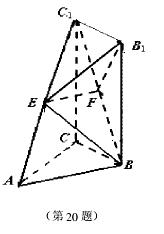 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;
(2)求证:平面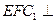 平面C1CBB1;
平面C1CBB1;
(3)求异面直线AB与EB1所成的角。
在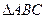 中,
中,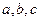 分别是角A、B、C的对边,
分别是角A、B、C的对边,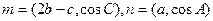 ,且
,且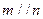
(1)求角A的大小;
(2)记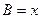 ,作出函数
,作出函数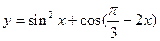 的图象。
的图象。
已知曲线
所围成的封闭图形的面积为
,曲线
的内切圆半径为
.记
为以曲线
与坐标轴的交点为顶点的椭圆.
(Ⅰ)求椭圆
的标准方程;
(Ⅱ)设
是过椭圆
中心的任意弦,
是线段
的垂直平分线.
是
上异于椭圆中心的点.
(1)若
(
为坐标原点),当点
在椭圆
上运动时,求点
的轨迹方程;
(2)若
是
与椭圆
的交点,求
的面积的最小值.
(满分14分)
设数列{an}的前n项和为Sn,且对任意正整数n,an+Sn=4096.
(1)求数列{an}的通项公式;
(2)设数列{log2an}的前n项和为Tn,求数列{Tn}从第几项起Tn<-12.
(本小题满分12分)东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本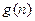 与科技成本的投入次数
与科技成本的投入次数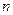 的关系是
的关系是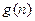 =
=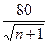 .若
.若 水晶产品的销售价格不
水晶产品的销售价格不 变,第
变,第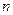 次投入后的年利润为
次投入后的年利润为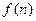 万元.①求出
万元.①求出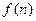 的表达式;②问从今年算起第几年利润最高?最高利润为多少万元?
的表达式;②问从今年算起第几年利润最高?最高利润为多少万元?