设椭圆C1和抛物线C2的焦点均在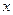 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
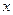 |
3 |
-2 |
4 |
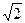 |
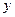 |
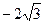 |
0 |
-4 |
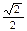 |
(1)求曲线C1,C2的标准方程;
(2)设直线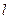 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且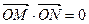 。请问是否存在直线
。请问是否存在直线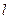 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线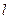 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)已知函数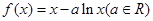
(Ⅰ)当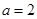 时,求曲线
时,求曲线 在点
在点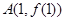 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数 单调区间
单调区间
(本小题满分12分)为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分按每度0.5元计算.
(1)设月用电x度时,应交电费y元.写出y关于x的函数关系式;
(2)小明家第一季度交纳电费情况如下:
则小明家第一季度共用电多少度?
已知函数 ,
, .且
.且 为奇函数,
为奇函数,
(1)求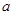 的值;
的值;
(1)若函数f(x)在区间(-1,1)上为增函数,且满足f(x-1)+f(x)<0,求x 的取值集合。
已知集合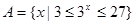 ,
, .
.
(1)分别求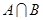 ,
,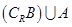 ;
;
(2)已知集合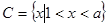 ,若
,若 ,求实数
,求实数 的取值集合.
的取值集合.
(本小题满分10分)已知函数f(x)=x2+ax+b的图象关于直线x=1对称.
(1)求实数a的值
(2)若f(x)的图象过(2,0)点,求x∈[0,3]时f(x)的值域.