阅读:
已知 、
、 ,
, ,求
,求 的最小值.
的最小值.
解法如下: ,
,
当且仅当 ,即
,即 时取到等号,
时取到等号,
则 的最小值为
的最小值为 .
.
应用上述解法,求解下列问题:
(1)已知 ,
, ,求
,求 的最小值;
的最小值;
(2)已知 ,求函数
,求函数 的最小值;
的最小值;
(3)已知正数 、
、 、
、 ,
, ,
,
求证: .
.
对任意实数x,矩阵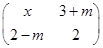 总存在特征向量,求m的取值范围.
总存在特征向量,求m的取值范围.
若矩阵A有特征值λ1=2,λ2=-1,它们所对应的特征向量分别为e1= 和e2=
和e2=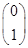 .
.
(1)求矩阵A.
(2)求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程.
已知矩阵A=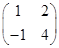 ,向量α=
,向量α=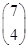 .
.
(1)求A的特征值λ1,λ2和对应的特征向量α1,α2.
(2)计算A5α的值.
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸缩变换.
(1)求矩阵M的特征值及相应的特征向量.
(2)求逆矩阵M-1以及椭圆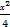 +
+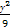 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.
已知矩阵M=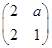 ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P'(-4,0),
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P'(-4,0),
(1)求实数a的值.
(2)求矩阵M的特征值及其对应的特征向量.