一家用电器开发公司研制出一种新型电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件．为了增加销量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件．
⑴ 求出月销售量y（万件）与销售单价x（元）之间的函数关系式；
⑵ 求出月销售利润z（万元）与销售单价x（元）之间的函数关系式，并在下面坐标系中，画出图象草图；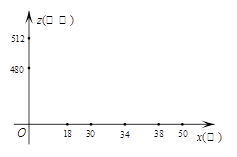
⑶ 为了使月销售利润不低于480万元，请借助⑵中所画图象进行分析，说明销售单价的取值范围．
观察下列图形的变化过程，解答以下问题：
如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E点，DF∥AB交AC于F点．
（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形．为什么？
已知：在平面直角坐标系中，点A（1，0），点B（4，0），点C在y轴正半轴上，且OB=2OC．
（1）试确定直线BC的解析式；
（2）在平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请直接写出点M的坐标．
已知m，n，d为一个直角三角形的三边长，且有
=8n﹣n2﹣16，求三角形三边长分别为多少？
（1）某水果批发商，批发苹果不少于80kg时，批发价为2.5元/kg，小张携现金2500元到这个市场采购苹果，并以批发价买进，设购买的苹果为xkg，小张付款后还剩余现金y元，写出y与x的函数关系式，并指出自变量x的取值范围．
（2）在直角坐标系中，直接画出函数y=|x+1|的图象．
我县某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降，今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．
（1）今年5月份A款汽车每辆售价多少万元？
（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？
（3）如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使（2）中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？