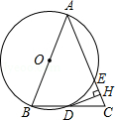
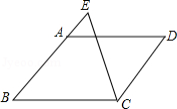
已知:如图,四边形 是平行四边形,延长 至点 ,使 .连接 ,求证: 平分 .
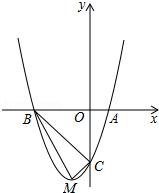
如图,顶点为 的抛物线 分别与 轴相交于点 , (点 在点 的右侧),与 轴相交于点 .
(1)求抛物线的函数表达式;
(2)判断 是否为直角三角形,并说明理由.
(3)抛物线上是否存在点 (点 与点 不重合),使得以点 , , , 为顶点的四边形的面积与四边形 的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.
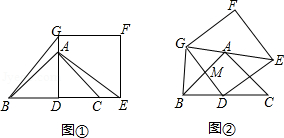
如图①, 为等腰直角 的高,点 和点 分别在正方形 的边 和 上,连接 , .
(1)求证: ;
(2)将正方形 绕点 旋转,当线段 经过点 时,(如图②所示)
①求证: ;
②设 与 交于点 ,若 ,求 的值.
某学校计划组织500人参加社会实践活动,与某公交公司接洽后,得知该公司有 , 型两种客车,它们的载客量和租金如表所示:
|
型客车 |
型客车 |
|
|
载客量(人 辆) |
45 |
28 |
|
租金(元 辆) |
400 |
250 |
经测算,租用 , 型客车共13辆较为合理,设租用 型客车 辆,根据要求回答下列问题:
(1)用含 的代数式填写下表:
|
车辆数(辆 |
载客量(人 |
租金(元 |
|
|
型客车 |
|
|
|
|
型客车 |
|
|
|
(2)采用怎样的租车方案可以使总的租车费用最低,最低为多少?
如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.