已知函数
，
为
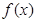的导函数。 （1）求函数
的单调递减区间；
（2）若对一切的实数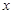
，有
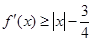成立，求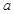
的取值范围；
（3）当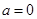
时，在曲线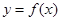
上是否存在两点
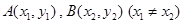，使得曲线在
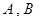两点处的切线均与直线
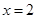交于同一点？若存在，求出交点纵坐标的最大值；若不存在，请说明理由．
（(本题15分)
在平面直角坐标系xOy中，已知点A(0,0)，B(-2,0)，C(-2,1)。设k为非零实数，矩阵M=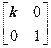
,N=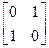
，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，
（1）求k的值。
（2）判断变换MN是否可逆，如果可逆，求矩阵MN的逆矩阵；如不可逆，说明理由．
（
某有奖销售将商品的售价提高120元后允许顾客有3次抽奖的机会，每次抽奖的方法是在已经设置并打开了程序的电脑上按“Enter”键，电脑将随机产生一个1~6的整数数作为号码，若该号码是3的倍数则顾客获奖，每次中奖的奖金为100元，运用所学的知识说明这样的活动对商家是否有利。
（
已知圆的极坐标方程为：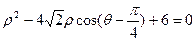
.
将极坐标方程化为普通方程，写出圆的参数方程。
若点P（x
,y）在该圆上，求x+y的最大值和最小值。
已知
，且正整数n满足
，
（1）求n ；
（2）若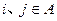
，是否存在
，当
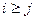时，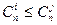
恒成立。若存在，求出最小的；
若不存在，试说明理由。
（3）
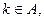若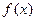
的展开式有且只有三个有理项，求
。
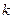已知矩阵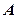
=
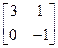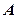，求的特征值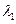
，
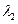及对应的特征向量
．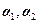