如图,地到火车站共有两条路径和,现随机抽取100位从地到火车站的人进行调查,调查结果如下:
| 所用时间(分钟) |
10~20 |
20~30 |
30~40 |
40~50 |
50~60 |
| 选择的人数 |
6 |
12 |
18 |
12 |
12 |
| 选择的人数 |
0 |
4 |
16 |
16 |
4 |
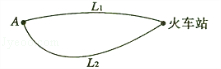
(1)试估计40分钟内不能 赶到火车站的概率;
(2)分别求通过路径和所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的 路径.
已知数列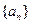 的前
的前
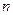 项和为
项和为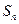 ,且
,且
(1)求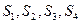 的值;
的值;
(2)猜想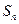 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
(本小题满分12分)
某公司在“2010年上海世博会知识宣传”活动中进行抽奖活动,抽奖规则是:在一个盒子中装有8张大小相同的精美卡片,其中2张印有“世博会欢迎您”字样,2张印有“世博会会徽”图案,4张印有“海宝”(世博会吉祥物)图案,现从盒子里无放回的摸取卡片,找出印有“海宝”图案的卡片表示中奖且停止摸卡。
(Ⅰ)求最多摸两次中奖的概率;
(Ⅱ)用 表示摸卡的次数,求
表示摸卡的次数,求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
已知 是奇函数,且在定义域(—1,1)内可导并满足
是奇函数,且在定义域(—1,1)内可导并满足 解关于m的不等式
解关于m的不等式
(本小题满分12分)
已知合集 的定义域为M,
的定义域为M, ,若
,若
(本小题满分13分)
已知函数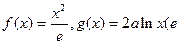 为自然对数的底数)
为自然对数的底数)
(1)求 的单调区间,若
的单调区间,若 有最值,请求出最值;
有最值,请求出最值;
(2)是否存在正常数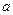 ,使
,使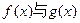 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出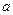 的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
的值,以及公共点坐标和公切线方程;若不存在,请说明理由。