已知函数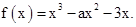
(1)若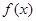 在区间
在区间 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(2)若 是
是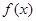 的极值点,求
的极值点,求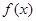 在
在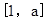 上的最大值;
上的最大值;
(3)在(2)的条件下,是否存在实数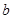 ,使得函数
,使得函数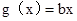 的图象与函数
的图象与函数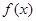 的图象恰有
的图象恰有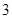 个交点,若存在,请求出实数
个交点,若存在,请求出实数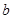 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
已知A={x|-1<x≤3},B={x|m≤x<1+3m}.
(1)当m=1时,求A∪B;
(2)若 ,求实数m的取值范围.
,求实数m的取值范围.
已知函数f(x)= 和函数g(x)=x|x﹣m|+2m﹣8,其中m为参数,且满足m≤5.
和函数g(x)=x|x﹣m|+2m﹣8,其中m为参数,且满足m≤5.
(1)若m=2,写出函数g(x)的单调区间(无需证明);
(2)若方程f(x)= 在x∈[﹣2,+∞)上有唯一解,求实数m的取值范围;
在x∈[﹣2,+∞)上有唯一解,求实数m的取值范围;
(3)若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得f(x2)=g(x1)成立,求实数m的取值范围.
已知函数f(x)=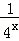 ﹣
﹣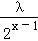 +3(﹣1≤x≤2).
+3(﹣1≤x≤2).
(1)若λ=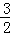 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若函数f(x)的最小值是1,求实数λ的值.
函数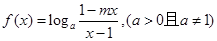 是奇函数.
是奇函数.
(1)求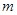 的值;
的值;
(2)判断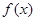 在区间
在区间 上单调性并加以证明;
上单调性并加以证明;
设二次函数f(x)=ax2+bx+c的图象过点(0,1)和(1,4),且对于任意的实数x,不等式f(x)≥4x恒成立.
(1)求函数f(x)的表达式;
(2)设g(x)=kx+1,若G(x)= 在区间[1,2]上是增函数,求实数k的取值范围。
在区间[1,2]上是增函数,求实数k的取值范围。