已知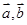 夹角为
夹角为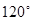 ,且
,且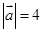 ,
,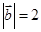 ,求:
,求:
(1)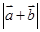 ; (2)
; (2)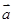 与
与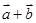 的夹角。
的夹角。
平行四边形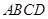 中,
中, ,
,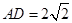 ,
, ,以
,以 为折线,把
为折线,把 折起,使平面
折起,使平面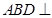 平面
平面 ,连结
,连结 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的大小.
的大小.
学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 |
女 |
|||||||
| 8 |
16 |
5 |
8 |
9 |
||||
| 8 |
7 |
6 |
17 |
2 |
3 |
5 |
5 |
6 |
| 7 |
4 |
2 |
18 |
0 |
1 |
2 |
||
| 1 |
19 |
0 |
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有1人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
在 中,
中,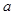 ,
, ,
,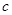 分别是角
分别是角 ,
, ,
, 的对边,向量
的对边,向量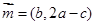 ,
, ,且
,且 //
// .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设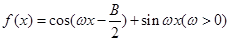 ,且
,且 的最小正周期为
的最小正周期为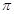 ,求
,求 在区间
在区间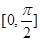 上的最大值和最小值.
上的最大值和最小值.
已知函数 .
.
(Ⅰ)设函数 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列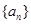 ,求证:
,求证: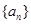 为等差数列;
为等差数列;
(Ⅱ)设函数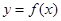 的图像的顶点到
的图像的顶点到 轴的距离构成数列
轴的距离构成数列 ,求
,求 的前
的前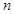 项和
项和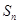 .
.
定义在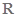 上的单调函数
上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有
(1)求证: 为奇函数;
为奇函数;
(2)若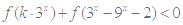 对任意
对任意 恒成立,求实数
恒成立,求实数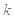 的取值范围.
的取值范围.