已知函数 ,
,
(1)求 在
在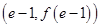 处切线方程;
处切线方程;
(2)求证:函数 在区间
在区间 上单调递减;
上单调递减;
(3)若不等式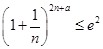 对任意的
对任意的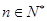 都成立,求实数
都成立,求实数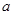 的最大值.
的最大值.
已知函数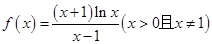 ,
,
(1)讨论函数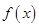 的单调性;
的单调性;
(2)证明: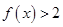 .
.
已知二次函数 若对于任意
若对于任意 ,恒有
,恒有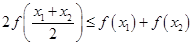 成立,不等式
成立,不等式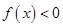 的解集为A,
的解集为A,
(1)求集合A;
(2)设集合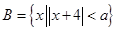 ,若集合B是集合A的子集,求
,若集合B是集合A的子集,求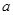 的取值范围.
的取值范围.
某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,
(1)求x和y的值;
(2)计算甲班七名学生成绩的方差;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:方差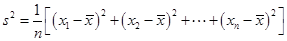 其中
其中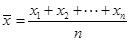
已知函数 (1)求
(1)求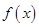 的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边
的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边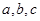 且满足
且满足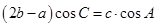 ,求
,求 的取值范围.
的取值范围.