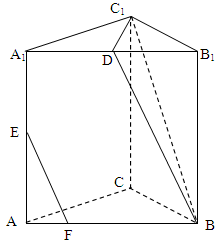
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且 .
.
(1)求证:EF∥平面BDC1;
(2)求证: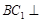 平面
平面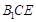 .
.
有以下三个不等式: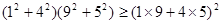 ;
; ;
; .
.
请你观察这三个不等式,猜想出一个一般性的结论,并证明你的结论。
设函数f(x)=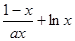 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(1)求正实数a的取值范围;
(2)比较 的大小,说明理由;
的大小,说明理由;
(3)求证: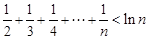 (n∈N*, n≥2)
(n∈N*, n≥2)
已知f(n)=(2n+7)3n+9,存在自然数m,使得对任意正整数n,都能使m整除f(n),猜测出最大的m的值。并用数学归纳法证明你的猜测是正确的。
如图,在三棱柱 中,
中, 侧面
侧面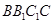 ,
, 为棱
为棱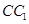 上异于
上异于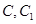 的一点,
的一点,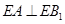 ,已知
,已知 ,求:
,求:
(Ⅰ)异面直线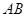 与
与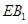 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.