已知函数f(x)=sinx,g(x)=mx- (m为实数).
(m为实数).
(1)求曲线y=f(x)在点P( ),f(
),f( )处的切线方程;
)处的切线方程;
(2)求函数g(x)的单调递减区间;
(3)若m=1,证明:当x>0时,f(x)<g(x)+ .
.
设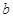 和
和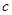 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(1)求方程 有实根的概率;
有实根的概率;
(2)求 的分布列和数学期望;
的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程 有实根的概率.
有实根的概率.
已知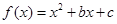 为偶函数,曲线
为偶函数,曲线 过点(2,5),
过点(2,5), 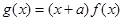 .
.
(1)若曲线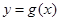 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围;
(2)若当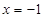 时函数
时函数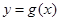 取得极值,确定
取得极值,确定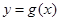 的单调区间.
的单调区间.
一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是 .
.
(1)求这名学生在途中遇到红灯的次数ξ的分布列;
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;
(3)这名学生在途中至少遇到一次红灯的概率.
为了解学生身高情况,某校以10%的比例对全校700名学生按性
别进行分层抽样调查,测得身高情况的统计图如下: 

(1)估计该校男生的人数;
(2)估计该校学生身高在170~185㎝之间的概率;
(3)从样本中身高在165~180㎝之间的女生中任选2人,求至少有1人身高在170~180㎝之间的概率;
在 中,
中, ,过点
,过点 的直线与其外接圆交于点
的直线与其外接圆交于点 ,交
,交 延长线于点
延长线于点 .
.
(1)求证: ; (2)若
; (2)若 ,求
,求