已知函数的导函数为偶函数,且曲线在点处的切线的斜率为.
(1)确定的值;
(2)若,判断的单调性;
(3)若有极值,求的取值范围.
某种产品的广告费支出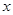 与销售额
与销售额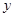 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
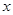 |
2 |
4 |
5 |
6 |
8 |
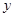 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率。
(参考数据: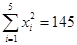
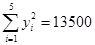
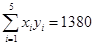 ,
,
参考公式:回归直线方程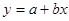 ,其中
,其中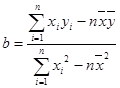 )
)
如图甲,在平面四边形ABCD中,已知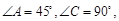
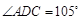 ,
,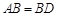 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD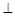 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.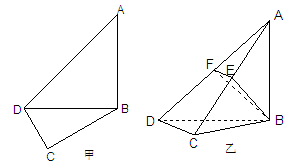
(Ⅰ)求证:DC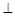 平面ABC;
平面ABC;
(Ⅱ)设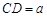 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
已知向量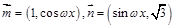
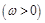 ,函数
,函数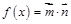 ,且
,且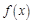 图象上一个最高点的坐标为
图象上一个最高点的坐标为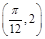 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为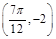 .
.
(1)求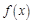 的解析式;
的解析式;
(2)在△ABC中, 是角A、B、C所对的边,且满足
是角A、B、C所对的边,且满足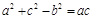 ,求角B的大
,求角B的大
小以及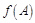 的取值范围.
的取值范围.
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为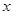 、
、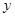 ,设
,设 为坐标原点,点
为坐标原点,点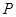 的坐标为
的坐标为 ,记
,记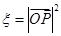 .
.
(1)求随机变量 =5的概率;
=5的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
在如图所示的几何体中,四边形 是菱形,
是菱形,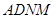 是矩形,平面
是矩形,平面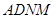 ⊥平面
⊥平面 ,
,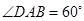 ,
,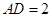 ,
,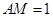 ,
,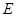 是
是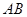 的中点.
的中点.
(Ⅰ) 求证: //平面
//平面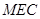 ;
;
(Ⅱ) 在线段 上是否存在点
上是否存在点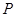 ,使二面角
,使二面角 的大小为
的大小为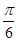 ?若存在,求出
?若存在,求出 的长
的长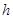 ;若不存在,请说明理由.
;若不存在,请说明理由.