已知椭圆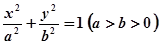 的离心率
的离心率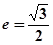 ,
,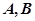 分别为椭圆的长轴和短轴的端点,
分别为椭圆的长轴和短轴的端点,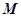 为
为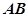 中点,
中点,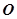 为坐标原点,且
为坐标原点,且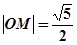 .
.
(1)求椭圆的方程;
(2)过点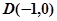 的直线
的直线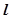 交椭圆于
交椭圆于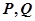 两点,求
两点,求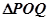 面积最大时,直线
面积最大时,直线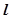 的方程.
的方程.
如图,直四棱柱 ABCD-A 1 B 1 C 1 D 1的底面是菱形, AA 1=4, AB=2,∠ BAD=60°, E, M, N分别是 BC , BB 1, A 1 D的中点.

(1)证明: MN∥平面 C 1 DE;
(2)求二面角 A-MA 1 -N的正弦值.
的内角A,B,C的对边分别为a,b,c,设 .
(1)求A;
(2)若 ,求sinC.
设a,b,c R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥ .
在直角坐标系xOy中,曲线C的参数方程为 (t为参数且t≠1),C与坐标轴交于A、B两点.
(1)求 ;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求直线AB的极坐标方程.
设函数 ,曲线 在点( ,f( ))处的切线与y轴垂直.
(1)求b.
(2)若 有一个绝对值不大于1的零点,证明: 所有零点的绝对值都不大于1.