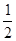已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的 ,总有
,总有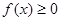 ;
;
② ;
;
③当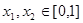 ,且
,且 时,
时,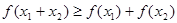 成立.
成立.
称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数 在区间
在区间 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在 ,使得
,使得 ,且
,且 ,求证:
,求证: .
.
国家统计局发布最新数据显示,2011年11月份全国副省级城市中CPI(消费指数)值位于前15位的城市具体情况如下表:
| 城市 |
CPI |
序号 |
城市 |
CPI |
序号 |
| 济南 |
105.2 |
1 |
青岛 |
104.7 |
2 |
| 广州 |
104.6 |
3 |
西安 |
104.4 |
4 |
| 哈尔滨 |
104.3 |
5 |
厦门 |
104.2 |
6 |
| 杭州 |
104.1 |
7 |
武汉 |
104.1 |
8 |
| 深圳 |
104.1 |
9 |
南京 |
103.9 |
10 |
| 长春 |
103.9 |
11 |
沈阳 |
103.6 |
12 |
| 大连 |
103.3 |
13 |
成都 |
103.0 |
14 |
| 宁波 |
102.6 |
15 |
(1)求这15个城市CPI值的平均值及众数
(2)完成下表:
| CPI |
[102.5,103.0) |
[103.0,103.5) |
[103.5,104.0) |
[104.0,104.5) |
[104.5,105.0) |
[105.0,105.5) |
| 频率 |
(3)从【103.0,104.0】区间内随机选取2城市,求恰有1个城市19.
已知向量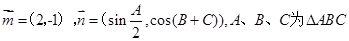 的内角,其所对的边分别为
的内角,其所对的边分别为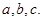
(1)当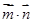 取得最大值时,求角A的大小;
取得最大值时,求角A的大小;
(2)在(1)的条件下,当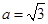 时,求
时,求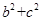 的取值范围。
的取值范围。
(本小题满分14分)已知数列{an}是以d为公差的等差数列,数列{bn}是以q为公比的等比数列
(Ⅰ)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3<5b2+a88-180,求整数q的值
(Ⅱ)在(Ⅰ)的条件下,试问数列{bn}中是否存在一项bk,使得b,k恰好可以表示为该数列中连续P(P∈N,P≥2)项和?请说明理由。
(Ⅲ)若b1=ar,b2=as≠ar, b3=at(其中t>s>r,且(s—r)是(t—r)的约数)求证:数列{bn}中每一项都是数列{an}中的项.
(本小题满分13分)已知圆G:x2+y2—2x—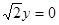 ,经过椭圆
,经过椭圆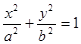 (a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为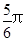 的直线l交椭圆于C、D两点.
的直线l交椭圆于C、D两点.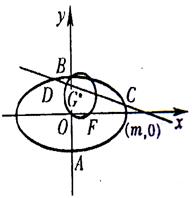
(Ⅰ)求椭圆方程
(Ⅱ)当右焦点在以线段CD为直径的圆E的内部,求实数m的范围
(本小题满分12分)已知函数y=f(x)在定义域(—1+∞)内满足f(o)=0,且f/(x)= 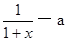 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)
(Ⅰ)求f(x)的表达式.
(Ⅱ)当a=1时,讨论f(x)的单调性
(Ⅲ)设h(x)=(ex—P)2+(x-P)2,证明:h(x)≥