甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望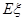 .
.
(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线 上至少取两个点,将其坐标记录于下表中:
上至少取两个点,将其坐标记录于下表中:
| x |
5 |
-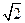 |
4 |
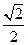 |
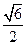 |
| y |
2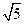 |
0 |
-4 |
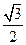 |
-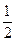 |

(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,-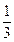 )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
(本小题满分12分)
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是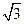 ,D是AC的中点.
,D是AC的中点.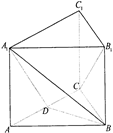
(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)求二面角A1-BD-A的大小;
(Ⅲ)求直线AB1与平面A1BD所成的角的正弦值.
(本小题满分12分 )
)
甲、乙两位学生参加数学建模竞赛培训,现分别从他们在培训期间参加的若干次预
赛成绩中随机抽取8次,记录如下:
甲:72 71 69 68 85 78 83 74
乙:82 85 70 65 73 70 80 75
(Ⅰ)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(Ⅱ)现要从中选派一人参加数学建模竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(Ⅲ)若将频率视为概率,对学生甲在今后的三次数 学建模竞赛成绩进行预测,记这三次成绩中高于80分的次数为ξ,求ξ的分布列
学建模竞赛成绩进行预测,记这三次成绩中高于80分的次数为ξ,求ξ的分布列 及数学期望Eξ.
及数学期望Eξ.
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c, 且
且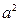 -
-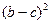 =(2
=(2 -
- )bc,sinA·sinB=
)bc,sinA·sinB= ,BC边上中线AM的长为
,BC边上中线AM的长为 .
.
(Ⅰ)求角A和角B的大小;
(Ⅱ)求△ABC的面积.
(本小题满分12分)
已知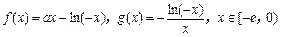 .
.
(1)讨论a =" –" 1时,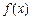 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下,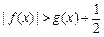 ;
;
(3)是否存在实数a,使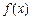 的最小值是3,如果存在,求出a的值;若不存在,
的最小值是3,如果存在,求出a的值;若不存在,
请说明理 由.
由.