如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题:
(1)79.5~89.5这一组的频率、频数分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均分.
把正整数按从小到大顺序排列成下列数表,数表中第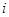 行共有
行共有 个正整数:
个正整数: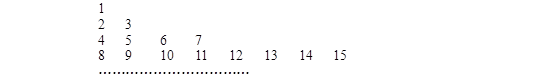
设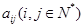 是位于数表中从上往下数第
是位于数表中从上往下数第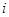 行、从左往右数第
行、从左往右数第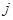 个数
个数
(1)若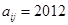 ,求
,求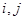 的值;
的值;
(2)记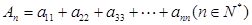 ,求数列
,求数列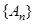 的通项公式;
的通项公式;
(3)猜想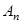 与
与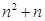 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
已知正方体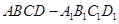 的棱长为1,点
的棱长为1,点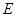 在
在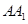 上,点
上,点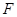 在
在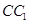 上,且
上,且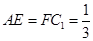
(1)求直线 与平面
与平面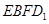 所成角的余弦值;
所成角的余弦值;
(2)用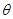 表示平面
表示平面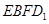 和侧面
和侧面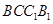 所成的锐二面角的大小,求
所成的锐二面角的大小,求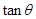 ;
;
(3)若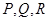 分别在
分别在 上,并满足
上,并满足 ,探索:当
,探索:当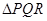 的重心为
的重心为 且
且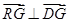 时,求实数
时,求实数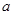 的取值范围.
的取值范围.
(1)试计算下列各式:(只需写出计算结果,不需写出计算过程)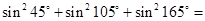 ____________
____________ ____________
____________ ____________
____________
(2)通过观察上述各式的计算规律,请你写出一般性的命题,并给出的证明
(参考公式: )
)
男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛,
分别求出下列情形有多少种选派方法?(以数字作答)
(1)男3名,女2名;
(2)队长至少有1人参加;
(3)至少1名女运动员;
(4)既要有队长,又要有女运动员.
已知复数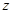 满足
满足 (
(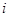 是虚数单位)
是虚数单位)
(1)求复数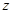 的虚部;
的虚部;
(2)若复数 是纯虚数,求实数
是纯虚数,求实数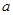 的值;
的值;
(3)若复数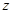 的共轭复数为
的共轭复数为 ,求复数
,求复数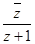 的模.
的模.