已知椭圆 的右焦点为
的右焦点为 ,离心率
,离心率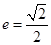 ,
,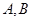 是椭圆上的两动点,动点
是椭圆上的两动点,动点 满足
满足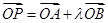 (其中实数
(其中实数 为常数).
为常数).
(1)求椭圆标准方程;
(2)当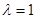 ,且直线
,且直线 过
过 点且垂直于
点且垂直于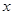 轴时,求过
轴时,求过 三点的外接圆方程;
三点的外接圆方程;
(3)若直线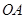 与
与 的斜率乘积
的斜率乘积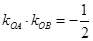 ,问是否存在常数
,问是否存在常数 ,使得动点
,使得动点 满足
满足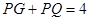 ,其中
,其中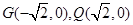 ,若存在求出
,若存在求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.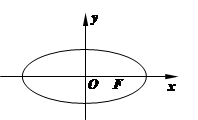
(本题15分)已知点 是椭圆E:
是椭圆E: (
( )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设A、B是椭圆E上两个动点, (
( ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;
(Ⅲ)在(Ⅱ)的条件下,当△PAB面积取得最大值时,求λ的值.
(本题15分)如图,在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点。
的中点。
(Ⅰ)证明: ;
;
(Ⅱ)证明: 平面
平面 ;
;
(Ⅲ)求二面角 的正切值.
的正切值.
(本题14分)口袋内有 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从
个白球.已知从
口袋中随机取出一个球是红球的概率是 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。
(Ⅰ)求 和
和 ;
;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 的分布列和期望
的分布列和期望 。
。
(本题14分)已知向量m = ,向量n =
,向量n = ,且m与n所成角为
,且m与n所成角为 ,其中A、B、C是
,其中A、B、C是 的内角。
的内角。
(Ⅰ)求角B的大小;
(Ⅱ)求 的取值范围。
的取值范围。
若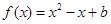 ,且
,且 ,
,
(1)求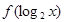 的最小值及相应 x的值;
的最小值及相应 x的值;
(2)若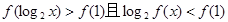 ,求x的取值范围.
,求x的取值范围.