如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
(1)画出“基本图形”关于原点O对称的四边形A1B1C1D1,并写出A1点的坐标,A1( , );
(2)画出“基本图形”关于x轴的对称图形A2B2C2D2,并写出B2点的坐标,B2( , ).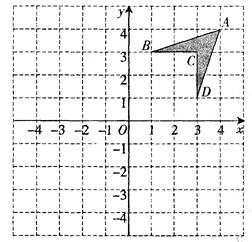
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若ÐDBC=30°,CD=4,求四边形ABED的面积.
如图,已知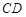 是⊙
是⊙ 的直径,弦
的直径,弦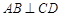 ,垂足为点
,垂足为点 ,点
,点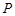 是
是 上一点,且
上一点,且 .试判断
.试判断 的形状,并说明你的理由.
的形状,并说明你的理由.
某校决定对初三学生进行体育成绩测试,成绩记入总分,同学们将根据自己平时的运动成绩确定自己的参考项目,下面是小亮同学的两个项目立定跳远和一分钟跳绳在近期连续五次测试的得分情况(立定跳远得分统计表和一分钟跳绳得分折线图):
立定跳远得分统计表
| 测试 日期 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| 得分 |
7 |
10 |
8 |
9 |
6 |

(1)请根据以上信息,分别将这两个项目的平均数、极差、方差填入下表:
| 统计量 |
平均数 |
极差 |
方差 |
| 立定跳远 |
8 |
||
| 一分钟跳绳 |
2 |
0.4 |
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的参考项目?请简述理由.
解方程:
A,B,C三个村庄在一条东西走向的公路沿线,如图所示,AB=2km,BC=3km,在B村的正北方向有一个D村,测得∠ADC=450今将△ACD区域规划为开发区,除其中4 km2的水塘外,均作为建筑或绿化用地,试求这个开发区的建筑及绿化用地的面积是多少?