如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于 点F,且∠CEF=2∠DAE.
(1)求证:直线EF为⊙O的切线;
(2)在点O的运动过程中,设DE=x,解决下列问题:
①求OD·CF的最大值,并求此时半径的长;
②试猜想并证明△CEF的周长为定值.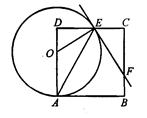
甘肃省省府兰州,又名金城,在金城,黄河母亲河通过自身文化的演绎,衍生和流传了独特的“金城八宝”美食,“金城八宝”美食中甜品类有:味甜汤糊“灰豆子”、醇香软糯“甜胚子”、生津润肺“热冬果”、香甜什锦“八宝百合”;其他类有:青白红绿“牛肉面”、酸辣清凉“酿皮子”、清爽溜滑“浆水面”、香醇肥美“手抓羊肉”,李华和王涛同时去品尝美食,李华准备在“甜胚子、牛肉面、酿皮子、手抓羊肉”这四种美食中选择一种,王涛准备在“八宝百合、灰豆子、热冬果、浆水面”这四种美食中选择一种.(甜胚子、牛肉面、酿皮子、手抓羊肉分别记为A,B,C,D,八宝百合、灰豆子、热冬果、浆水面分别记为E,F,G,H)
(1)用树状图或表格的方法表示李华和王涛同学选择美食的所有可能结果;
(2)求李华和王涛同时选择的美食都是甜品类的概率.
在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:
已知:直线l和l外一点P.
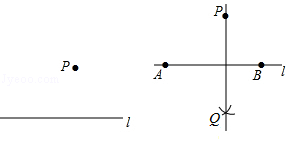
求作:直线l的垂线,使它经过点P.
作法:如图:(1)在直线l上任取两点A、B;
(2)分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;
(3)作直线PQ.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是:
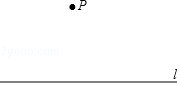
(2)已知,直线l和l外一点P,
求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
如图1,在平面直角坐标系中,抛物线 y= x 2+ x﹣ 与 x轴交于点 A、 B(点 A在点 B右侧),点 D为抛物线的顶点,点 C在 y轴的正半轴上, CD交 x轴于点 F,△ CAD绕点 C顺时针旋转得到△ CFE,点 A恰好旋转到点 F,连接 BE.
(1)求点 A、 B、 D的坐标;
(2)求证:四边形 BFCE是平行四边形;
(3)如图2,过顶点 D作 DD 1⊥ x轴于点 D 1,点 P是抛物线上一动点,过点 P作 PM⊥ x轴,点 M为垂足,使得△ PAM与△ DD 1 A相似(不含全等).
①求出一个满足以上条件的点 P的横坐标;
②直接回答这样的点 P共有几个?

如图1,在△ ABC中, AB= AC,⊙ O是△ ABC的外接圆,过点 C作∠ BCD=∠ ACB交⊙ O于点 D,连接 AD交 BC于点 E,延长 DC至点 F,使 CF= AC,连接 AF.
(1)求证: ED= EC;
(2)求证: AF是⊙ O的切线;
(3)如图2,若点 G是△ ACD的内心, BC• BE=25,求 BG的长.

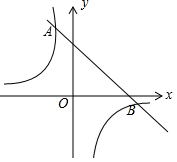
如图,一次函数 y= k 1 x+ b的图象与反比例函数 y= 的图象相交于 A、 B两点,其中点 A的坐标为(﹣1,4),点 B的坐标为(4, n).
(1)根据图象,直接写出满足 k 1 x+ b> 的 x的取值范围;
(2)求这两个函数的表达式;
(3)点 P在线段 AB上,且 S △ AOP: S △ BOP=1:2,求点 P的坐标.