已知 ,
,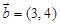 ,
,
(1)若 与
与 垂直,求
垂直,求 的值;
的值;
(2)若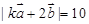 ,求
,求 的值.
的值.
已知等差数列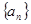 的第二项为8,前10项和为185。
的第二项为8,前10项和为185。
(1)求数列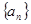 的通项公式;
的通项公式;
(2)若从数列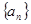 中,依次取出第2项,第4项,第8项,……,第
中,依次取出第2项,第4项,第8项,……,第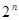 项,……按原来顺序组成一个新
项,……按原来顺序组成一个新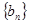 数列,试求数列
数列,试求数列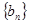 的通项公式和前n项的和
的通项公式和前n项的和
已知△ABC中,各点的坐标分别为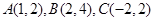 ,求:
,求:
(1)BC边上的中线AD的长度和方程;
(2)△ABC的面积.
已知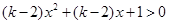 对一切
对一切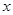 恒成立,求实数
恒成立,求实数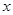 的取值范围.
的取值范围.
已知f(x)的定义域为(0,+∞),且满足f(2)=1,f(xy)=f(x)+f(y),又当x2>x1>0时,f(x2)>f(x1).
(1)求f(1)、f(4)、f(8)的值;
(2)若有f(x)+f(x-2)≤3成立,求x的取值范围.
已知函数 .
.
(1)确定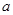 的值,使
的值,使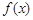 为奇函数;
为奇函数;
(2)当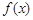 为奇函数时,求
为奇函数时,求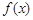 的值域。
的值域。