如图,△ABC和△ADC有公共边AC,E是公共边上一点.
(1)已知:AB=AD,BE=DE. 求证:△ABC≌△ADC.
(2)已知:∠1=∠2,∠3=∠4.求证:∠5=∠6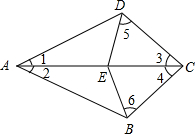
(·湖北孝感)已知关于x的一元二次方程:
(1)试判断原方程根的情况;
(2)若抛物线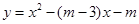 与
与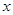 轴交于
轴交于 两点,则
两点,则 ,
, 两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:
两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示: )
)
(·湖北武汉,17题,分)(本题8分)已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式求,关于x的不等式kx+3≤6的解集.
(·湖北黄冈,16题,分)已知A,B两件服装的成本共500元,鑫洋服装店老板分别以30%和20%的利润率定价后进行销售,该服装店共获利130 元,问A,B两件服装的成本各是多少元?
(·湖北黄冈,15题,分)解不等式组: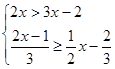 .
.
(·湖北鄂州,20题,8分)关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根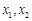 .
.
(1)求实数k的取值范围.
(2)若方程两实根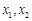 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.