以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,-5),点M的极坐标为(4,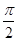 ).若直线l过点P,且倾斜角为
).若直线l过点P,且倾斜角为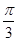 ,圆C以M为圆心, 4为半径.
,圆C以M为圆心, 4为半径.
(1)求直线l的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
(本小题满分12分) 已知二次函数 的图象经过原点,且
的图象经过原点,且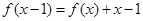 。
。
(1)求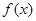 的表达式.
的表达式.
(2)设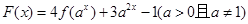 ,当
,当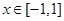 时,
时,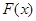 有最大值14,试求
有最大值14,试求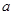 的值.
的值.
(本小题满分12分)已知函数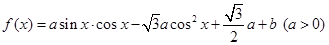
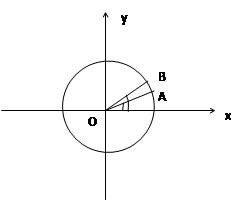
(1)写出函数的最小正周期和对称轴;
(2)设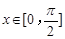 ,
,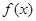 的最小值是
的最小值是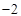 ,最大值是
,最大值是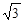 ,求实数
,求实数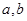 的值.
的值.
(本题满分12分)某民营企业生产A、B两种产品,根据市场调查和预测,A产品的利润y与投资额x成正比,其关系如图1所示;B产品的利润y与投资额x的算术平方根成正比,其关系如图2所示(利润与投资额的单位均为万元). (1)分别将A、B两种产品的利润表示为投资额的函数关系式;(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?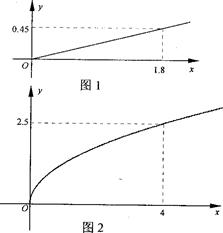
(本小题满分12分)探究函数 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
16 |
10 |
8.34 |
8.1 |
8.01 |
8 |
8.01 |
8.04 |
8.08 |
8.6 |
10 |
11.6 |
15.14 |
… |
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数 在区间上递增.当
在区间上递增.当 时,
时, .
.
(2)证明:函数 在区间(0,2)递减.
在区间(0,2)递减.
(3)思考:函数 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(本小题满分12分)如图,在平面直角坐标系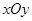 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角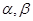 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为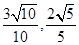 .
.
(1)求 的值; (2)求
的值; (2)求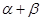 的值.
的值.