已知集合
，
，
，
.
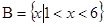（1）求
； （2）若
，求实数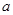
的取值范围.
在数列
和
中，
，
，
，其中
且
，
.
（Ⅰ）若
，
，求数列的前
项和；
（Ⅱ）证明：当
时，数列中的任意三项都不能构成等比数列；
（Ⅲ）设
，
，试问在区间
上是否存在实数
使得
.若存在，求出的一切可能的取值及相应的集合
；若不存在，试说明理由.
已知焦点在
轴，顶点在原点的抛物线
经过点P（2，2），以上一点
为圆心的圆过定点
（0，1），记
为圆
与
轴的两个交点．
（1）求抛物线
的方程；
（2）当圆心在抛物线上运动时，试判断
是否为一定值？请证明你的结论；
（3）当圆心在抛物线上运动时，记
，
，求
的最大值．
已知函数
,点
为一定点,直线
分别与函数
的图象和
轴交于点
,
,记
的面积为
.
（1）当
时,求函数的单调区间；
（2）当
时, 若
,使得
, 求实数
的取值范围.
某中学校本课程共开设了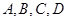
共
门选修课,每个学生必须且只能选修
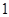门选修课,现有该校的甲、乙、丙
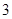名学生.
（Ⅰ）求这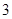名学生选修课所有选法的总数；
（Ⅱ）求恰有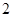
门选修课没有被这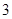名学生选择的概率；
（Ⅲ）求
选修课被这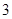名学生选择的人数
的分布列和数学期望.
上恒有f(x)
－3成立，求实数a 的取值范围.