设函数fn(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围;
(3)在(1)的条件下,设xn是fn(x)在 内的零点,判断数列x2,x3,…,xn,…的增减性.
内的零点,判断数列x2,x3,…,xn,…的增减性.
已知椭圆C: 的焦距为4,其长轴长和短轴长之比为
的焦距为4,其长轴长和短轴长之比为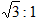 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设F为椭圆C的右焦点,T为直线 上纵坐标不为0的任意一点,过F作TF的垂
上纵坐标不为0的任意一点,过F作TF的垂
线交椭圆C于点P,Q.
(ⅰ)若OT平分线段PQ(其中O为坐标原点),求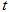 的值;
的值;
(ⅱ)在(ⅰ)的条件下,当 最小时,求点T的坐标.
最小时,求点T的坐标.
已知数列 中,
中,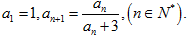
(1)求数列 的通项公式
的通项公式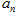 ;
;
(2)若数列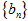 满足
满足 数列
数列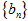 的前
的前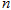 项和为
项和为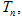 若不等式
若不等式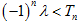 对一切
对一切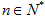 恒成立,求
恒成立,求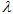 的取值范围.
的取值范围.
如图所示,在四棱锥PABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.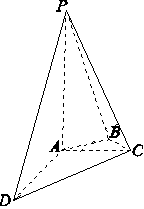
(1)证明:PC⊥AD;
(2)求二面角A-PC-D的正弦值.
已知函数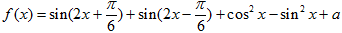 的在区间
的在区间 上的最小值为0.
上的最小值为0.
(Ⅰ)求常数a的值;
(Ⅱ)当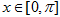 时,求使
时,求使 成立的x的集合.
成立的x的集合.