某体育用品专卖店今年3月初用4000元购进了一批“中考体能测试专用绳”，上市后很快售完．该店于3月中旬又购进了和第一批数量相同的专用绳，由于第二批专用绳的进价每根比第一批提高了10元，结果进第二批专用绳共用了5000元．
（1）第一批专用绳每根的进货价是多少元？
（2）若第一批专用绳的售价是每根60元，为保证第二批专用绳的利润率不低于第一批的利润率，那么第二批专用绳每根售价至少是多少元？（提示：利润=售价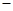
进价，利润率=
）
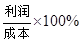如图所示，点B，E，C，F在同一直线上，AB=DE，∠B=∠DEF，BE=CF．求证：AC=DF．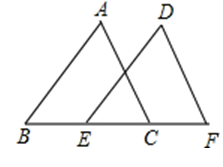
某种上屏每天的销售利润y（元）与销售单价x（元）之间满足关系：y=ax2+bx-75.其图像如图所示.
销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
销售单价在什么范围时，该种商品每天的销售利润不低于16元？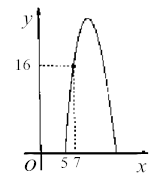
几个小伙伴打算去音乐厅观看演出，他们准备用360元购买门票.下面是两个小伙伴的对话：
根据对话的内容，请你求出小伙伴们的人数.
甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9
填写下表：
| 平均数 |
众数 |
中位数 |
方差 |
|
| 甲 |
8 |
？ |
8 |
0.4 |
| 乙 |
？ |
9 |
？ |
3.2 |
教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？
如果乙再射击1次，命中8环，那么乙的射击成绩的方差.（填“变大”、“变小”或“不变”）.
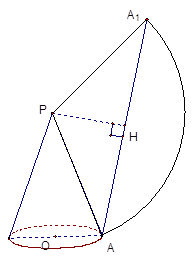
如图，圆锥底面半径OA=10㎝，母线PA=30㎝.由底面周长上一点A出发绕其侧面一周的最短路线长度是多少？