设项数均为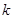 (
(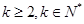 )的数列
)的数列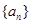 、
、 、
、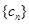 前
前 项的和分别为
项的和分别为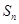 、
、 、
、 .已知
.已知 ,且集合
,且集合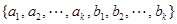 =
=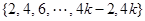 .
.
(1)已知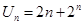 ,求数列
,求数列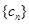 的通项公式;
的通项公式;
(2)若 ,求
,求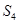 和
和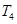 的值,并写出两对符合题意的数列
的值,并写出两对符合题意的数列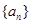 、
、 ;
;
(3)对于固定的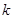 ,求证:符合条件的数列对(
,求证:符合条件的数列对(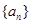 ,
, )有偶数对.
)有偶数对.
某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元的赔偿(假设每辆车最多只赔偿一次).设这三辆车在一年内发生此种事故的概率分别为
,且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;
(2)获赔金额
的分布列与期望.
设
(1)求
的最大值及最小正周期;
(2)若锐角
满足
,求
的值.
设
,对任意实数
,记
.
(I)求函数
的单调区间;
(II)求证:(ⅰ)当
时,
对任意正实数
成立;
(ⅱ)有且仅有一个正实数
,使得
对任意正实数
成立.
已知数列
中的相邻两项
,是关于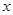 的方程
的两个根,且
.
的方程
的两个根,且
.
(I)求
,
,
,
;
(II)求数列
的前
项和
;
(Ⅲ)记
,
,
求证: .
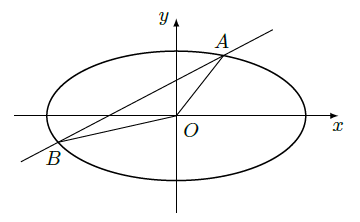
如图,直线
与椭圆
交于
两点,记
的面积为
.
(I)求在
的条件下,
的最大值;
(II)当
时,求直线
的方程.