保持正弦曲线上所有点的纵坐标不变,横坐标缩短为原来的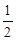 ,再将图像沿
,再将图像沿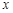 轴向右平移
轴向右平移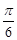 个单位,得到函数
个单位,得到函数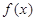 的图像.
的图像.
(1)写出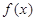 的表达式,并计算
的表达式,并计算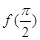 .
.
(2)求出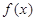 在
在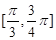 上的值域.
上的值域.
(本小题满分10分)已知命题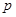 :
: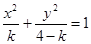 表示焦点在
表示焦点在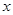 轴上的椭圆,命题
轴上的椭圆,命题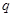 :
: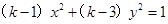 表示双曲线.若
表示双曲线.若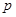 或
或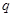 为真,
为真,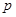 且
且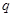 为假,求
为假,求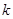 的取值范围.
的取值范围.
已知抛物线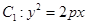 与椭圆
与椭圆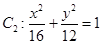 在第一象限的交点为B,O为坐标原点,A是椭圆右顶点,
在第一象限的交点为B,O为坐标原点,A是椭圆右顶点,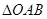 的面积为
的面积为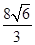 .
.
(1)求抛物线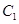 的方程;
的方程;
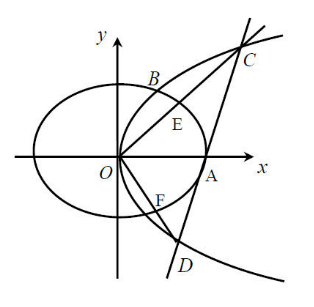
(2)过A点作直线 交
交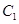 于C,D两点,射线OC,OD分别交
于C,D两点,射线OC,OD分别交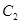 于E,F两点,记
于E,F两点,记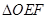 和
和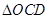 的面积分别为
的面积分别为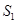 和
和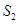 ,问是否存在直线
,问是否存在直线 ,使得
,使得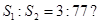 若存在,求出直线
若存在,求出直线 方程,若不存在,请说明理由.
方程,若不存在,请说明理由.
已知抛物线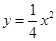 ,圆
,圆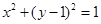 ,过点
,过点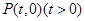 作不过原点O的直线PA,PB分别与抛物线和圆相切,A,B为切点(A为抛物线切点,B为圆的切点).
作不过原点O的直线PA,PB分别与抛物线和圆相切,A,B为切点(A为抛物线切点,B为圆的切点).
(1)求点A,B坐标;
(2)求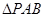 面积.
面积.
已知椭圆C: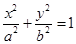
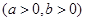 的左焦点为
的左焦点为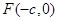 ,点
,点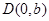 ,直线DF的斜率为
,直线DF的斜率为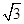 .
.
(1)求椭圆的离心率;
(2)设过点F的直线交椭圆于A,B两点,过点P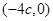 作与直线AB的倾斜角互补的直线
作与直线AB的倾斜角互补的直线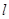 交椭圆于M,N两点,问
交椭圆于M,N两点,问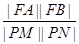 是否为定值,若是求出此定值,若不是说明理由.
是否为定值,若是求出此定值,若不是说明理由.
圆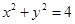 的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P.
的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P.
(1)求点P坐标;
(2)焦点在x轴上的椭圆过点P,且与直线 交于A,B两点,若
交于A,B两点,若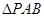 的面积为2,求椭圆的标准方程.
的面积为2,求椭圆的标准方程.