已知曲线 的直角坐标方程为
的直角坐标方程为 ,以坐标原点
,以坐标原点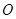 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.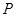 是曲线
是曲线 上一点,
上一点,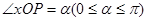 ,将点
,将点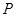 绕点
绕点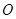 逆时针旋转角
逆时针旋转角 后得到点
后得到点 ,
, ,点
,点 的轨迹是曲线
的轨迹是曲线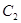 .
.
(Ⅰ)求曲线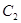 的极坐标方程.
的极坐标方程.
(Ⅱ)求 的取值范围.
的取值范围.
(本小题10分)
设全集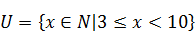 ,
, 和
和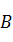 都是全集
都是全集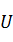 的子集,且有
的子集,且有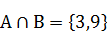 ,
,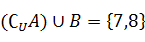 ,
,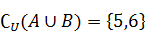 ,求集合
,求集合 与
与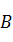 .
.
(本题14分)某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2-6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2-6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点.注:1个百分点=1%)
| 年份 |
二月 |
三月 |
四月 |
五月 |
六月 |
| 2010 |
2.7 |
2.4 |
2.8 |
3.1 |
2.9 |
| 2011 |
4.9 |
5.0 |
x |
y |
z |
(本题12分)某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.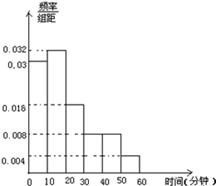
(1)若抽取的50个样本是用系统抽样的方法得到,
且第一段的号码为006,则第五段抽取的号码是什么?
(2)若从50个样本中属于第4组和第6组的所有人
中随机抽取2人,设他们上学时间分别为a、b,求满足
|a-b|>10的事件的概率;
(3)设学校配备的校车每辆可搭载40名学生,请根
据抽样的结果估计全校应有多少辆这样的校车?
(本题12分,)将编号为1、2、3、4的四个小球放入甲、乙、丙三只盒子内.
(1)若三只盒子都不空,且3号球必须在乙盒内有多少种不同的放法;
(2)若1号球不在甲盒内,2号球不在乙盒内,有多少种不同放法。(均须先列式再用数字作答)
(本题12分,)有6名同学站成一排,求:
(1)甲不站排头也不站排尾有多少种不同的排法:
(2)甲、乙、丙不相邻有多少种不同的排法.(均须先列式再用数字作答)