已知 ,
,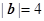 ,且向量
,且向量 与
与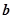 不共线.
不共线.
(1)若 与
与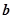 的夹角为
的夹角为 ,求
,求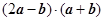 ;
;
(2)若向量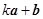 与
与 互相垂直,求
互相垂直,求 的值.
的值.
(本小题满分13分)把一个正方体的表面涂上红色,在它的长、宽、高上等距离地各切三刀,则大正方体被分割成64个大小相等的小正方体,将这些小正方体均匀地搅混在一起,如果从中任取1个,求下列事件的概率
(1)事件A=“这个小正方体各个面都没有涂红色”
(2)事件B=“这个小正方体只有1个面涂红色”
(3)事件C=“这个小正方体至少2个面涂红色”
(本小题满分12分)
已知p:方程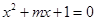 有两个不等的负根;
有两个不等的负根;
q:方程 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,
求m的取值范围.
(本小题满分12分)四棱锥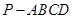 的底面是正方形,
的底面是正方形,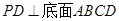 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=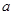 ,
,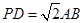
(Ⅰ)求证:平面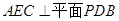 ;
;
(Ⅱ)若E为PB的中点时,求AE与平面PDB所成的角的大小.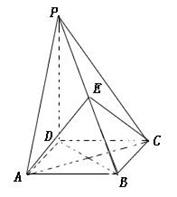
某校从参加高二年级期中考试的学生中抽出60名学生,将其成绩(均为整数)分成六段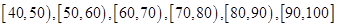 后,画出如下部分频率分布直方图。观察图形,回答下列问题:
后,画出如下部分频率分布直方图。观察图形,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分以上为及格);
(3)估计这次考试的平均分。
(本小题满分12分)
有4张面值相同的债券,其中有2张中奖债券.
(1)有放回地从债券中任取2次,每次取出1张,计算取出的2张都是中奖债券的概率.
(2)无放回地从债券中任取2次,每次取出1张,计算取出的2张中至少有1张是中奖债券的概率.