已知等差数列{an}满足a3=5,a5﹣2a2=3,又等比数列{bn}中,b1=3且公比q=3.
(1)求数列{an},{bn}的通项公式;
(2)若cn=an+bn,求数列{cn}的前n项和Sn.
(本小题满分10分)选修4-4:坐标系与参数方程
将圆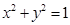 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线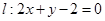 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与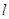 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
(本小题满分10分)选修4-1:几何证明选讲.
如图,在 中,
中,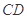 是
是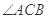 的角平分线,
的角平分线,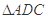 的外接圆交
的外接圆交 于点
于点 ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)当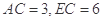 时,求
时,求 的长.
的长.
(本小题满分12分)已知函数f(x)=alnx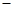 ax
ax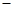 3(a∈R)。
3(a∈R)。
(Ⅰ)求f(x)的单调区间
(Ⅱ)设a=-1,求证:当x∈(1,+∞)时,f(x)+2>0
(Ⅲ)求证: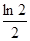 ·
·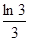 ·
·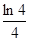 ……
……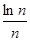 <
<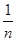 (n∈N+且n≥2)
(n∈N+且n≥2)
(本小题满分12分)设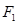 ,
,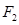 分别是椭圆
分别是椭圆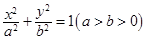 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且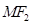 与x轴垂直,直线
与x轴垂直,直线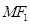 与C的另一个交点为N.
与C的另一个交点为N.
(Ⅰ)若直线MN的斜率为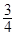 ,求C的离心率;
,求C的离心率;
(Ⅱ)若直线MN在y轴上的截距为2,且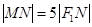 ,求a,b.
,求a,b.
(本小题满分12分)如图,在四棱锥P—ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.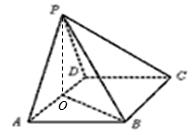
(Ⅰ)若PA=PD,求证:平面POB⊥平面PAD;
(Ⅱ)试问在线段BC上是否存在点M,使DM//面POB,如存在,指出M的位置,如不存在,说明理由.