已知 ,
, ,求下列各式的值:
,求下列各式的值:
(1)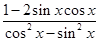
(2)
设函数f(x)=x2+|x-2|-1,x∈R.
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的最小值.
(满分10分)已知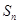 为数列
为数列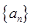 的前
的前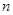 项和,
项和,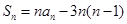 (
(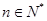 ),且
),且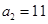 .
.
(1)证明数列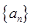 是等差数列,并求其前
是等差数列,并求其前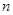 项和
项和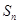 ;
;
(2)设数列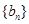 满足
满足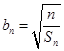 ,求证:
,求证: .
.
(满分10分)已知函数
(1) 时,解关于
时,解关于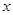 的不等式
的不等式 ;
;
(2)当 时,若对任意的
时,若对任意的 ,不等式
,不等式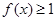 恒成立,求实数
恒成立,求实数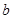 的取值范围;
的取值范围;
(满分10分) 在锐角 中,
中,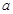 ,
, ,
, 分别为内角
分别为内角 ,
,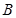 ,
, 所对的边,且满足
所对的边,且满足
(Ⅰ)求角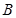 的大小;
的大小;
(Ⅱ)若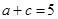 ,且
,且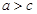 ,
, ,求
,求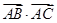 的值.
的值.
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在所给的直角坐标系中画出它们的散点图
(2)并求这些数据的线性回归方程 =bx+a.
=bx+a.
附:线性回归方程 中,
中,
其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.