已知数列 满足:
满足: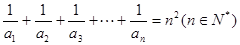 ,令
,令 ,
, 为数列
为数列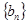 的前
的前 项和。
项和。
(1)求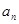 和
和 ;
;
(2)对任意的正整数 ,不等式
,不等式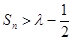 恒成立,求实数
恒成立,求实数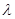 的取值范围.
的取值范围.
已知函数f(x)=kx+b的图象与x、y轴分别相交于点A、B,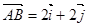 (
(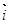 、
、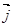 分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
(1)求k、b的值;
(2)当x满足f(x)> g(x)时,求函数 的最小值.
的最小值.
已知方程 的方程
的方程 ,直线
,直线

(1)求 的取值范围; (2)若圆
的取值范围; (2)若圆 与直线
与直线 交于P、Q两点,且以PQ为直径的圆恰过坐标原点,求实数m的值.
交于P、Q两点,且以PQ为直径的圆恰过坐标原点,求实数m的值.
汽车制造厂生产A、B、C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
Z |
| 标准型 |
300 |
450 |
600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求Z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有一辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2。把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率。
已知直线 与圆
与圆 相交于点
相交于点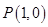 和点
和点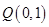 。
。
(1)求圆心 所在的直线方程; (2)若圆
所在的直线方程; (2)若圆 的半径为1,求圆
的半径为1,求圆 的方程。
的方程。
.提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当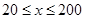 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(Ⅰ)当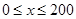 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度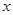 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)