在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.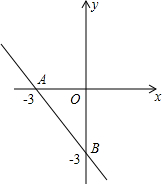
我市某水产养殖中心,2014年鱼塘饲养鱼苗10千尾,平均每千尾鱼的产量为103千克,2015年计划继续向鱼塘投放鱼苗,每多投放鱼苗1千尾,每千尾的产量将减少50千克.
(1)今年应投放鱼苗多少千尾,可以使总产量达到10450千克?
(2)该水产养殖中心今年应投放鱼苗多少千尾,可以达到最大总产量?最大总产量是多少千克?
为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为30°,然后他向气球方向前进了40m,此时观测气球,测得仰角为60°,如图,点A、B表示小明两次观测气球时眼睛的位置,若小明的眼睛离地面1.5m,请你帮助他计算出气球的高度.(结果保留根号)
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
如图,一个可以自由转动的均匀转盘被分成了4等份,每份内均标有数字,小明和小亮商定了一个游戏,规则如下:
(1)连续转动转盘两次;
(2)将两次转盘停止后指针所指区域内的数字相加(当指针恰好停在分格线上时视为无效,重转);
(3)若数字之和为奇数,则小明赢;若数字之和为偶数,则小亮赢.
请用“列表”或“画树状图”的方法分析一下,这个游戏对双方公平吗?并说明理由.
某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
| 类别 |
科普类 |
教辅类 |
文艺类 |
其他 |
| 册数(本) |
168 |
105 |
m |
32 |
(1)表格中字母m的值等于;
(2)扇形统计图中“教辅类”所对应的圆心角α的度数为°;
(3)该校2014年八年级有600名学生,请你估计该年级学生共借阅教辅类书籍约多少本?