设f(x)=ax3+bx+c为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1)求a,b,c的值;
(2)求函数f(x)的单调递增区间,极大值和极小值,并求函数f(x)在[-1,3]上的最大值与最小值.
(本小题12分)某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高 (米),塔所在的山高
(米),塔所在的山高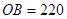 (米),
(米), (米),图中所示的山坡可视为直线
(米),图中所示的山坡可视为直线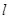 且点
且点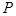 在直线
在直线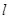 上,
上, 与水平地面的夹角为
与水平地面的夹角为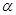 ,
, ,试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
,试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)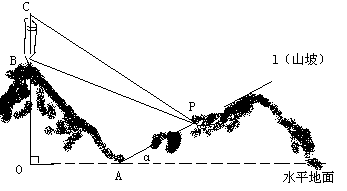
(本小题12分) 已知函数
 的图象过点
的图象过点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在△ 中,若
中,若 ,求
,求 的取值范围.
的取值范围.
(本小题12分)已知在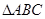 中,
中,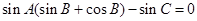 ,
,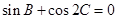 ,求角
,求角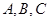 的大小.
的大小.
(本小题12分)已知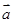 、
、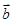 、
、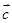 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中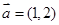 .
.
(Ⅰ)若|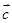 |
|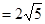 ,且
,且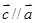 ,求
,求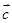 的坐标;
的坐标;
(Ⅱ)若|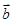 |=
|=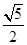 ,且
,且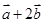 与
与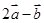 垂直,求
垂直,求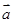 与
与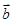 的夹角
的夹角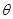 .
.
(本小题12分)如图,在 中,设
中,设 ,
, ,又
,又 ,
, ,向量
,向量 ,
, 的夹角为.
的夹角为.
(Ⅰ)用 表示
表示 ;
;
(Ⅱ)若点 是
是 边的中点,直线
边的中点,直线 交
交 于
于 点,求
点,求 .
.