(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
先化简,再求值: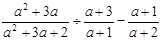 ,其中
,其中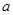 =
=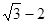 .
.
课本回顾
如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为.
问题拓展
如图,在矩形ABCD内,已知⊙O1与⊙O2互相外切,且⊙O1与边AD、DC相切,⊙O2与边AB、BC相切.若AB=4,BC=3,⊙O1与⊙O2的半径分别为r,R.求O1O2的值.
灵活运用
如图,某市民广场是半径为60米,圆心角为90°的扇形AOB,广场中两个活动场所是圆心在OA、OB上,且与扇形OAB内切的半圆☉O1、☉O2,其余为花圃.若这两个半圆相外切,试计算当两半圆半径之和为50米时活动场地的面积.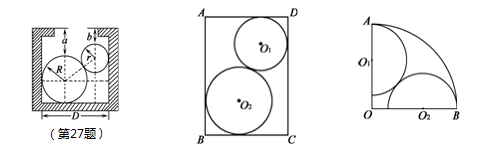
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2)求出(1)中外接圆圆心P的坐标;
(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请直接写出点Q 坐标;如果不存在,请说明理由.
已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b=;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=- x+b,求n的值.
x+b,求n的值.
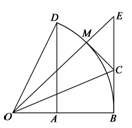
如图,以O为圆心的弧 度数为60 o,∠BOE=45o,DA⊥OB,EB⊥OB.
度数为60 o,∠BOE=45o,DA⊥OB,EB⊥OB.
(1)求 的值;
的值;
(2)若OE与 交于点M,OC平分∠BOE,连接CM.说明:CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明:CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.