已知函数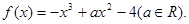
(1)若函数 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为
(2)设 的导函数是
的导函数是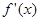 ,在(1)条件下,若
,在(1)条件下,若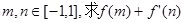 的最小值;
的最小值;
(3)若存在 的取值范围.
的取值范围.
已知椭圆C:
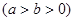 和直线L:
和直线L: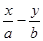 ="1," 椭圆的离心率
="1," 椭圆的离心率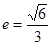 ,坐标原点到直线L的距离为
,坐标原点到直线L的距离为 。
。
(1)求椭圆的方程;
(2)已知定点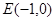 ,若直线
,若直线
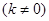 与椭圆C相交于M、N两点,试判断是否存在
与椭圆C相交于M、N两点,试判断是否存在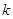 值,使以MN为直径的圆过定点E?若存在求出这个
值,使以MN为直径的圆过定点E?若存在求出这个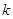 值,若不存在说明理由。
值,若不存在说明理由。
如图,在三棱柱ABC-A1B1C1中,已知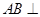 侧面
侧面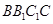 ,AB=BC=1,BB1=2,∠BCC1=
,AB=BC=1,BB1=2,∠BCC1=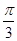 .
.
(1) 求证:C1B⊥平面ABC;
(2)设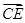 =l
=l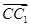 (0≤l≤1),且平面AB1E与BB1E所成的锐二面角
(0≤l≤1),且平面AB1E与BB1E所成的锐二面角
的大小为30°,试求l的值.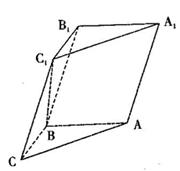
从天气网查询到衡水历史天气统计 (2011-01-01到2014-03-01)资料如下: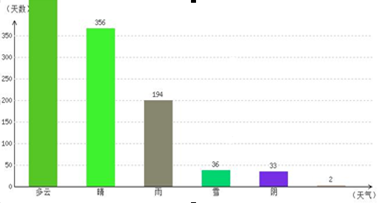
自2011-01-01到2014-03-01,衡水共出现:多云507天,晴356天,雨194天,雪36天,阴33天,其它2天,合计天数为:1128天。
本市朱先生在雨雪天的情况下,分别以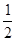 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为2元或40元;在非雨雪天的情况下,他以90%的概率骑自行车上班,每天交通费用0元;另外以10%的概率打出租上班,每天交通费用20元。(以频率代替概率,保留两位小数.参考数据:
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为2元或40元;在非雨雪天的情况下,他以90%的概率骑自行车上班,每天交通费用0元;另外以10%的概率打出租上班,每天交通费用20元。(以频率代替概率,保留两位小数.参考数据: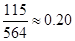 )
)
(1)求他某天打出租上班的概率;
(2)将他每天上班所需的费用记为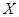 (单位:元),求
(单位:元),求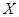 的分布列及数学期望。
的分布列及数学期望。
已知等差列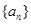 的前n项和为
的前n项和为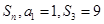
(1)求数列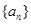 的通项公式:
的通项公式:
(2)若函数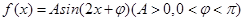 在
在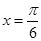 处取得最大值,且最大值为a2,求函数
处取得最大值,且最大值为a2,求函数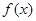 的解析式。
的解析式。
在平面直角坐标系中,以原点为极点,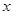 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线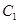 的方程为
的方程为 (
(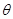 为参数),曲线
为参数),曲线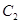 的极坐标方程为
的极坐标方程为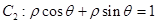 ,若曲线
,若曲线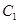 与
与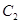 相交于
相交于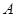 、
、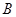 两点.
两点.
(1)求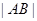 的值;
的值;
(2)求点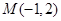 到
到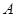 、
、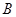 两点的距离之积.
两点的距离之积.